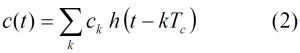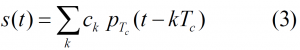Binary Offset Carrier Signals are a particular case of BCS signals with a representation vector formed by +1’s and -1’s alternating in a particular defined way. Two notations [E. Rebeyrol et al., 2005] [1] can be found in the literature to define the BOC signals. We describe them shortly in the following lines.
The first model defines the BOC modulation as the result of multiplying the PRN code with a sub-carrier which is equal to the sign of a sine or a cosine waveform, yielding so-called sine-phased or cosine-phased BOC signals respectively as shown in [J.W. Betz, 2001] [2], [L.R.Weill, 2003] [3], [J. Godet, 2001] [4] and [E. Rebeyrol et al., 2005] [1]. According to this definition, the expression of the sine-phased BOC signal would be:
-
- with
where
-
- ck is the code sequence waveform,
- fs is the sub-carrier frequency,
- and
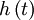 is the Non Return to Zero (NRZ) code materialization with value 1 over the support
is the Non Return to Zero (NRZ) code materialization with value 1 over the support 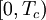 .
.
The second model defines the BOC modulation as follows:
where 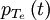 describes the chip waveform and is broken up into n rectangular pulses of duration Tc / n with amplitude ±1. It is important to note that in this case the sine-phasing or cosine-phasing is considered as part of the chip waveform definition. This convention has been introduced in [A.R. Pratt and J.I.R. Owen, 2003a] [5] and [J.W. Betz, 2001][2].
describes the chip waveform and is broken up into n rectangular pulses of duration Tc / n with amplitude ±1. It is important to note that in this case the sine-phasing or cosine-phasing is considered as part of the chip waveform definition. This convention has been introduced in [A.R. Pratt and J.I.R. Owen, 2003a] [5] and [J.W. Betz, 2001][2].
No matter what definition we choose to describe the BOC modulation in the time domain, the BOC signal is commonly referred to as BOC(fs, fc) where 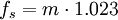 and
and 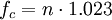 so that generally one only says BOC(m, n) for simplicity. Moreover, unless it is indicated in a different way, when we talk about BOC signals we will always mean the sine-phased variant.
so that generally one only says BOC(m, n) for simplicity. Moreover, unless it is indicated in a different way, when we talk about BOC signals we will always mean the sine-phased variant.
출처 : http://www.navipedia.net/index.php/Binary_Offset_Carrier_(BOC)
'Technology > by Lab' 카테고리의 다른 글
| 오일러 정리 증명 (0) | 2014.04.27 |
|---|---|
| 푸리에 변환 계수(Fourier Transform Coefficient) 증명 (0) | 2014.04.27 |
| SCI, SCIE 논문 IF(impact factor, 논문인용지수), JCR 조사 (0) | 2013.06.02 |
| jitter (0) | 2013.05.28 |
| pulse shaping (0) | 2013.05.28 |
| 그림(.jpg, .gif, .bmp ,png), PDF파일을 문자(.txt), 한글(.hwp), 워드(.doc)로 변환하기(구글 OCR 사용법) (2) | 2013.05.10 |
| Fourier Transform(푸리에 변환) step function (1) | 2013.04.26 |